タイムマシンの初歩教材について（大学一年生が一般相対論の問題を解ける物理学教科書）

1 『理工系物理学』と『誤差論』

中学生のとき、同級生の青木勝樹君とタイムマシンについて夢中になって話した。しかし、青木勝樹君は光速の壁で諦めてしまった。私は諦めきれずにいたが、大学生になってローレンツ変換の説明を読んでいて諦めた。青木勝樹君については別れの時空選択を参照。
私が大学を卒業する前に、兄が千葉大学教養部に化学の講師として赴任した。千葉大学教養部に鐸木康孝教授がいた。兄は、鐸木教授から、大学教養部での物理の教育の改善について、時々聞いた。物理の中で最も誤解が多いのは、相対論だという。
鐸木教授は1979年に『理工系物理学』を開成出版から出版した。私は兄から『理工系物理学』を受け取った。『理工系物理学』では、ローレンツ変換を使わずに特殊相対論を説明しているのである。これには驚いた。マックスウェルの方程式から、スカラーポテンシャルとベクトルポテンシャルが4次元のベクトルを形成することを導いているのである。この導出方法がゾンマーフェルトの『電磁気学』にも記されていることは、後で知った。相対論にローレンツ変換が不要だという事実は衝撃だった。ローレンツ変換は4次元ベクトルを導き出すための手段の一つにすぎないのである。
『理工系物理学』の相対論の章の初めには、4次元空間が一種の非ユークリッド空間であると書かれている。光速の壁に悩んだのは、4次元空間をユークリッド空間であると思い込んでいたからであった。ローレンツ変換が相対論に不要であり、4次元空間がユークリッド空間ではないとなると、タイムマシンの可能性が出てくる。しかし、私は社会人になっていて、『理工系物理学』を学ぶ時間はなかった。

David DeutschとMichael Lockwoodの「タイムマシンの量子物理学」The Quantum Physics of Time travelが日経サイエンス1994年5月号に発表された。翻訳は佐藤勝彦氏である。その要約をここに引用する。
「現在の”常識”によれば、タイムマシンはありえないことになっている。例えば、ある人が過去にさかのぼって祖父を殺してしまったとすると、その人自身が存在しえないことになってしまうからだ。これ以外にもさまざまなパラドックスが生じてしまうために、「タイムマシンはありえない」ということになっている。
しかし、著者たちは、現代物理学の法則はタイムマシンを禁じているわけではない、と主張する。確かに、決定論である古典物理学では、どうしてもパラドックスが発生してしまう。しかし、超ミクロな世界では、こうした古典物理学は近似にさえなりえず、量子物理学こそが世界を正しく記述する。このような世界では、1957年にエベレット（Hugh Everet)が提案した「多重宇宙」の考えが広く認知されている。
多重宇宙とは、SFでおなじみのパラレルワールド(並行宇宙)のことである。量子論を多重宇宙に応用すると、話は決定論的になる。しかし、同時に、パラドックスはすべて解消してしまうのである。先の例では、別の宇宙からやってきた孫によって祖父が殺される宇宙では、祖父の殺人者は誕生しなかった、というわけである。」

要約に続いて4次元空間について述べ、「閉じた時間的曲線CTC」(closed timelike curve)について述べている。それに続いてエベレットの多重宇宙論により、パラドックスが解消されると述べている。閉じた時間的な線をつくるのがタイムマシンなのである。
以上、「タイムマシンの量子物理学」は、ローレンツ変換を使わずにタイムマシンを説明している。『理工系物理学』がローレンツ変換を使わずに相対論を説明している価値が分かる。

鐸木康孝著『理工系物理学』（開成出版）の目次は、次のとおりである。
「０章 ベクトル テンソル
00ベクトル 01ビベクトル 02トリベクトル 03積分定理 04テンソル 05スピノル。
１章 古典力学
10エネルギー・運動量・角運動量 11線形振動(A) 12線形振動(B) 13 電磁場の中の荷電粒子の運動 14ビリアル定理と断熱定理 15弾性散乱 16剛体の運動 17回転する剛体に対する相対運動 18フェルマの定理 19最小作用の原理。
２章 古典電磁気学
20電気量と電流 21起電力と電束 22電束と起磁力 24ポテンシャル 25エネルギー・運動量・角運動量 26最小作用の原理 27静電場 28定磁場 29線形公式
３章 波
30正弦波 31波動方程式 32ホイヘンスの原理 33波の散乱 34電磁波 35電磁波の例 36非線形波。
４章 相対論
40電磁場の法則の4次元形式(A) 41電磁場の法則の4次元形式(B) 42ミンコフスキー空間 43加速度運動 44質点の運動方程式 45一般相対論。
５章 量子力学
50電磁場と光子 51核力場とπ中間子 52化学結合力の場と電子 53スピン 54量子条件 55物理量と測定値 56原子の構造(A) 57原子の構造(B) 58分子の構造 59光の量子力学。
６章 統計力学
60ブラウン運動(A) 61ブラウン運動(B) 62カノニカル分布 63グランドカノニカル分布 64量子統計力学 65熱力学。
７章 物性物理
70個体の結晶構造 71固体の熱容量 72誘電性 73結晶内の電子 74電気伝導 75磁性。
８章 原子核
80シェル構造 81核反応 82核の崩壊 83加速器 84恒星内核反応 85宇宙線。
９章 素粒子
90素粒子の分類 91サカタ模型とクォーク 92ハドロンの励起状態。」

『理工系物理学』の目次を見ると、0章にスピノルがあるのが注目される。ロジャー・ペンローズの『皇帝の新しい心』（みすず書房、1994年、林一訳）にはリーマン球面の説明がある。『理工系物理学』のスピノルの説明はリーマン球面と関係がある。
『理工系物理学』が出版された1979年では私は、0章にスビノルが出てくる重要さを理解できなかった。21世紀になって『皇帝の新しい心』を読んで、その重要さを理解できた。『皇帝の新しい心』の英語版が出版されたのは1989年である。1979年の出版で最初の章でスビノルを説明している『理工系物理学』の先進性は驚くべきである。
目次に書かれている項目の他にも『理工系物理学』には、ラーモアの運動、断熱不変量、ゲージ変換、クライン・ゴルドンの波動方程式、ドゥシトゥル空間、シュワルツシルト空間、ブラックホール、ホワイトホール、ユカワポテンシャル、ディラックの方程式等の高度な事項が出てくる。相対論の章には光子ロケットを取り扱う問題がある。超光速粒子タキオンを取り扱う問題もある。
内容が高度でも、鐸木康孝著『理工系物理学』は、大学一年生・二年生が使うのを目的としている教科書である。使用している数学は大学二年の前期までの内容であり、それを超す数学は附録に説明がある。フーリエ級数、複素積分、エルミートは出てこない。ユニタリー行列の例は練習問題に出てくるけど、ユニタリー行列を学ぶのは後でよい。これらを学ぶ以前にスピノル他の重要な概念を学べるように『理工系物理学』は工夫されているのである。この教科書で学べば、大学一年生・二年生でもタイムマシンの初歩を学べるのである。
天羽優子氏は岩波書店の『科学』2007年12月号の「心にのこる一冊」で、『理工系物理学』を紹介していて、その「はじめに」を紙面の半分近くを使って引用している。以下はその引用部分の一部分である。
「物理学の理論はすべて近似である。ケプラーの法則に従って運行する惑星は一つもないし、ニュートンの法則に従って運動する質点とか剛体とかいうものは一つもない。正しいか、正しくないか、ということは、物理学では問題にならない。問題になるのは精度である。精度が低いか、高いか、どれだけ高くなったか、ということだけが物理学の関心事であり、それが物理学を前進させる原動力である。精度が極端に悪く、誤差の極めて大きな理論に対して、これは誤であるという判定が行われることはある。しかし、この理論は正しいという判定が行われたことは今まで一度もないし、これからも当分はないであろう。正しい理論が出現するのは、物理学が前進をやめるときすなわち滅亡するときである。」

以上のように鐸木康孝氏は精度を重視している。それゆえ、一瀬正巳著『誤差論』も並行して学ぶ教材としてあげておく。
一瀬正巳著『誤差論』（培風館）の目次は次のとおりである。
「第１章 誤差伝播の概念と近似計算
§1．誤差 §2．間接測定における誤差の測定 §3．精度の斉一 §4．観測値間の数値計算における誤差の転移 §5．近似式の使用 §6．計算の諸手段 §7．計算様式の形式化および検算
第２章 最小二乗法
§8．誤差の分布 §9．最確値 §10．観測値の信頼度 §11．二乗平均誤差および確率誤差の残差よりの算出 §12．重率が異なる観測値の組合せ §13．観測値の函数に対する誤差伝播関係 §14．函数的関係にある多くの未知所求量の間接測定に最小二乗法を適用すること §15．間接測定における二乗平均誤差または確率誤差 §16．未知量が２個の場合の取扱い §17．未知量が３個の場合の取扱い §18．未知量間の函数が線形でない場合 §19．未知量に条件がある場合 §20．条件づき測定の例
第３章 実験式
§21．実験式 §22．実験曲線 §23．直線y=α＋βt §24．直線y=βt §25．対数曲線 §26．指数曲線およびその関係曲線 §26.α 一般抛物線、双曲線およびその関係曲線 §27．多項式（有理整式） §28．観測記録の平滑化 §29．Fourier級数、調和解析 §30．連続値近似表式（全域近似表式） §31．補間法」
§13までは容易に理解できた、練習問題も解ける。§13までは大学一年生の学習範囲である。§14以降は難しくなる。私は大学卒業後に薄っぺらな『誤差論』だけは読み通したいと思い、挑戦した。§17で挫折した。しかし、精度についての知識は§13までで充分である。
タイムマシンの学習以外でも、鐸木康孝著『理工系物理学』（開成出版）と一瀬正巳著『誤差論』（培風館）は大学一年生・二年生の物理学の教科書として最適である。

２ 大学一年生が読めるタイムマシンの論文は「閉じた時間的な線の近くの量子力学」の最初の６頁

鐸木康孝氏は、『理工系物理学』の「この教科書を採用される先生方へ」の最後ででも、重要な事を述べられている。
「しょせん、教科書は死んだ素材である。この素材に命を吹きこみ、生きた講義の中に活用していただけるならば、著者としては望外の喜びである。」
『理工系物理学』を学ぶ人のほとんどは独習であろう。死んだ素材になるのを防ぎたいものである。解決策の一つは論文を読むことである。
大学に入学してから一年は、David Deutsch著「Quantum mechanics near closed timelike kines（閉じた時間的な線の近くの量子力学）」の最初の6頁（全体では20頁）がよい。David Deutschは「Quantum mechanics near closed timelike kines（閉じた時間的な線の近くの量子力学）」を発表した3年後に「タイムマシンの量子物理学The Quantum Physics of Time travel」を発表している。「タイムマシンの量子物理学The Quantum Physics of Time travel」はMichael Lockwoodと共著である。
鐸木康孝氏著『理工系物理学』には「閉じた時間的な線」という言葉は出てこない。閉じた時間的な線を理解するにはDavid Deutsch著「Quantum mechanics near closed timelike kines（閉じた時間的な線の近くの量子力学）」の最初の6頁（全体では20頁）が必要である。
「閉じた時間的な線の近くの量子力学」のPDFをＱｕａｎｔｕｍ　ｍｅｃｈａｎｉｃｓ　ｎｅで見つけてダウンロードした。

2.1 「閉じた時間的な線の近くの量子力学」の第1章「計算の量子論を応用」を学ぶ時の注意

第1章「計算の量子論を応用」2頁半は図を使って、閉じた時間的な線を説明している。world line世界線という言葉が出てくる。必要な相対論の知識は『ランダウ＝リフシッツ理論物理学教程』の『場の古典論』の§1「相互作用の伝版速度』と§2「世界間隔」と§3「固有時間」だけである。さらに、『理工系物理学』の附録の「A4 ベクトル空間の定義」と「A1 双対ベクトル空間・計量」を読んでおくと分かりやすい。鐸木康孝著『理工系物理学』の目的の一つは『ランダウ＝リフシッツ理論物理学教程』を読みやすくすることである。『ランダウ＝リフシッツ理論物理学教程』の『場の古典論』の§1「相互作用の伝版速度』と§2「世界間隔」と§3「固有時間」は鐸木康孝著『理工系物理学』を読んでいなくても理解できる。
「閉じた時間的な線の近くの量子力学」の第1章「計算の量子論を応用」を学んでおくと、『ランダウ＝リフシッツ理論物理学教程』の『場の古典論』の§1「相互作用の伝版速度』と§2「世界間隔」と§3「固有時間」と『理工系物理学』の附録の「A4 ベクトル空間の定義」と「A1 双対ベクトル空間・計量」を生きた知識にできるということでもある。たったこれだけでも、生きた知識にできるのは価値がある。
「閉じた時間的な線の近くの量子力学」の第1章と第2章「時間順序侵害の古典的パラドックス」を学んでから鐸木康孝著『理工系物理学』の相対論までを学ぶとよい。
「閉じた時間的な線の近くの量子力学」は1ビットまたは数ビットを持つ粒子を使って議論している。コンピュータの知識は16進数演算と論理演算の機能を持つ関数電卓で充分である。
第1章「計算の量子論を応用」では図とgateを理解するのが重要である。出てくるgateはmeasurement gateである。
英文は難しい。読むだけでは理解できない。繰り返し書き取りする必要がある。私は１０回した。以降の章も同様である。

2.2 「閉じた時間的な線の近くの量子力学」の第2章「時間順序侵害の古典的パラドックス」を学ぶ時の注意

排他的論理和が「時間順序侵害の古典的パラドックス」の説明に使われている。排他的論理和を使った式の説明にketという単語が出てくる。記号|>のことである。第2章ではket|>の定義は知らなくてよい。気にしなくてよい。
「閉じた時間的な線の近くの量子力学」の第2章ではproper time固有時という用語が出てくる。『場の古典論』の§3「固有時間」を読めばよい。

2.3 「閉じた時間的な線の近くの量子力学」の第３章「パラドックスの量子計算分析」のＵを展開してみよう。

閉じた時間的な線をつくることを優先して学びたい人は「閉じた時間的な線の近くの量子力学」のこれ以降を後回しにしてよい。
「閉じた時間的な線の近くの量子力学」の第３章「パラドックスの量子計算分析」ではＵが次のように定義されている。

Ｕ＝Σ｜ｘ＋ｙ＞｜ｘ＞＜ｘ｜＜ｙ｜ （＋の上には点がついていて排他的論理和）

ｘ、ｙの値は０か１に限定されている。ｘ＝０，ｙ＝０；ｘ＝０，ｙ＝１；ｘ＝１，ｙ＝０；ｘ＝１，ｙ＝１を代入すればよいのである。
Ｕはユニタリ行列だと思われる。ユニタリ行列をまだ学んでいなければ、ブルーバックスの『数学用語小事典』のユニタリ行列の項を読めばよい。Ｕの定義以降の数式に展開したUを代入してみよう。
鐸木康孝著『理工系物理学』には「ユニタリ行列」という用語は出てこない。しかし、第０章「ペクトル テンソル」の問題０９（スビノルの問題）にはユニタリ行列の条件を満たす行列が出てくる。これは容易に確認できる。
「閉じた時間的な線の近くの量子力学」の第３章「パラドックスの量子計算分析」には、○の中に×が入っている記号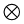が出てくる。テンソル積と思われる。鐸木康孝著『理工系物理学』の第０章「ペクトル テンソル」には○の中に×が入っている記号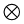を使っているテンソル積の説明が出てくる。『スミルノフ高等数学教程』の「群の線型表現」という節の「行列の直積」という項には、「ここに定義されている行列の直積はテンソル積またはクロネッカー積とも呼ばれている」という注がついている。テンソル積は行列の直積と考えてよいようである。
「閉じた時間的な線の近くの量子力学」の第３章「パラドックスの量子計算分析」の冒頭を理解する鍵は鐸木康孝著『理工系物理学』の第０章「ペクトル テンソル」である。附録Ａ０「ベクトル空間の定義」と併せて理解しておくとよい。
第３章「パラドックスの量子計算分析」ではディラックのベクトル記号ブラケットが本格的に使われている。ブラケットについてはディラック著『量子力学』（岩波書店）の§６までを読めばよい。また、次のことを知っておくとよい。
「｜Ｂ＞がケット・ベクトル、＜Ａ｜がブラ・ペクトル、＜Ａ｜Ｂ＞が内積であることはよく知られている。ところが、｜Ａ＞｜Ｂ＞とか｜Ｂ＞＜Ａ｜が出てくると、とまどってしまう。
｜Ａ＞｜Ｂ＞に左からブラ・ベクトル＜Ｐ｜をかけた＜Ｐ｜Ａ＞｜Ｂ＞の＜Ｐ｜Ａ＞は内積でありスカラーである。＜Ｐ｜Ａ＞｜Ｂ＞は｜Ｂ＞を＜Ｐ｜Ａ＞倍したケット・ベクトルなのである。
｜Ｂ＞＜Ａ｜に左からブラ・ベクトル＜Ｐ｜をかけた＜Ｐ｜Ｂ＞＜Ａ｜の＜Ｐ｜Ｂ＞は内積でありスカラーである。＜Ｐ｜Ｂ＞＜Ａ｜は＜Ａ｜を＜Ｐ｜Ｂ＞倍したブラ・ベクトルなのである。」
２次元のｄｅ Ｓｉｔｔｅｒ空間の計量を求める問題を先にするか、Ｕの展開を先にするかは各人の自由である。。
第３章「パラドックスの量子計算分析」のこの先については、行列のトレースを知っておく必要がある。大学一年生の範囲を超えると思われる。

3 鐸木康孝著『理工系物理学』のド・ジッター空間の計量の問題は大学一年生が解ける、マレット著『タイム・トラベラー』参照

2010年7月30日、朝刊に祥伝社のロナルド・L・マレット著『タイム・トラベラー』の広告があった。それまでロナルド・L・マレットを知らなかった。
『タイム・トラベラー』の第5章にはファインマン図、第6章にはド・ジッター空間、第10章にはプラックホールが出てくる。鐸木康孝著『理工系物理学』ではド・ジッター空間とプラックホールは一般相対論に、ファインマン図は量子力学に出てくる。
「閉じた時間的な線の近くの量子力学」の第2章「時間順序侵害の古典的パラドックス」までを読んでから、マレット著『タイム・トラベラー』を読みながら鐸木康孝著『理工系物理学』の相対論・量子力学・統計力学までを学ぶとよい。
鐸木康孝著『理工系物理学』の電磁気学は物理法則の精度にやかましいので、自然と『誤差論』を学びたくなる。
鐸木康孝著『理工系物理学』の相対論の章末には2次元のde Sitter空間の計量を求める問題がある。偏微分と全微分の知識があれば、解くことが可能な問題である。すなわち、大学一年生が解くことが可能な問題である。私は解けた。
ここまでを私はタイムマシンの初歩教材または大学一年生向けの教材と考えている。「閉じた時間的な線の近くの量子力学」の第3章「パラドックスの量子計算分析」以降は大学一年生の範囲を超えると思う。

4 「回転円筒と帯域的な因果関係侵害の可能性」

『タイム・トラベラー』の第11章にはFrank J.Tipler著「Rotating cylinders and the possibility of global causality violation（回転円筒と帯域的な因果関係侵害の可能性）」が紹介されている。
この論文の序文に「closed timelike line閉じた時間的な線」と「time machineタイムマシン」が出てくる。
これはＫａｚｕｍｏｔｏ　Ｉｇｕｃｈｉ’ｓ　ｂｌでダウンロードできる。

5 『タイム・トラベラー』の著者マレット博士の論文

『タイム・トラベラー』の第１１章と第１３章にはマレット博士の論文「Weak Gravitational Field of the Electromagnetic Radiation in a Ring Laser(電磁波の弱い重力場とリングレーザー)」と「The Gravitational Field of a Circulating Ligt Beam(循環する光線の重力場)」が紹介されている。タイムマシンの初歩教材ではなく本命の教材です。「The Gravitational Field of a Circulating Ligt Beam(循環する光線の重力場)」の序文に「closed timelike line閉じた時間的な線」が出てくる。

この二つの論文「Weak Gravitational Field of the Electromagnetic Radiation in a Ring Laser(電磁波の弱い重力場とリングレーザー)」と「The Gravitational Field of a Circulating Ligt Beam(循環する光線の重力場)」はＲｏｎａｌｄ　Ｍａｌｌｅｔｔ　−　Ｗｉｋでダウンロードできる。
この二つの論文「Weak Gravitational Field of the Electromagnetic Radiation in a Ring Laser(電磁波の弱い重力場とリングレーザー)」と「The Gravitational Field of a Circulating Ligt Beam(循環する光線の重力場)」の英文は難しくない。
David Deutsch著「Quantum mechanics near closed timelike kines（閉じた時間的な線の近くの量子力学）」の最初の6頁（全体では20頁）を読んだ後は、「Weak Gravitational Field of the Electromagnetic Radiation in a Ring Laser(電磁波の弱い重力場とリングレーザー)」を読むのが良い。
2021年4月5日、「Weak Gravitational Field of the Electromagnetic Radiation in a Ring Laser(電磁波の弱い重力場とリングレーザー)」を理解するために、ディラック著「一般相対性理論」を読み始めた。テンソルの添え字の上げ下げが出てくる。習熟するのには日数がかかる・

参考 タイムマシンのための量子計算の論文

「閉じた時間的な線の近くの量子力学」はDeutschの次の二つの論文の続きである。

Quantum theory,the Church-Turing principle and the universal quantum computer。Ｑｕａｎｔｕｍ　ｔｈｅｏｒｙ，ｔｈｅ　Ｃでダウンロードできる。2005年に入手。プリント済み。大きな英和辞典にも出てこない難しい英単語が出てくる。stochasticとかbijective。多宇宙を使って量子計算が能だと主張している。Everettの多宇宙解釈を支持している。

Quantum computational networks。2020年3月2日にプリント。

「ペンローズの量子脳裏論」で説明できる体験を別れの時空選択に書いています。

このサイトの頁構成図
日出島哲雄(秀島哲雄)

2018年10月1日に「2019年3月31日Yahoo!ジオシティーズのサービスを終了」というメールが来た。
恐ろしい。
そのメールにはホームページの引越先が6つ紹介されていた。
さくらのレンタルサーバー、LOLIPOP、XSERVER、XREA、忍者ホームページ、StarServerであった。
ジオシティーズにあるホームページと同じホームページを引越先のサーバーに同じアップロードすることはできる。
新しいホームページは検索されて出てくるようになるまで長い月日を必要とするのである。
さくらのレンタルサーバー、LOLIPOP、XSERVERは有料なので使う気がしない。
XREA、忍者ホームページ、StarServerには無料サーバーがあるので、この三つから選ぶことになる。
忍者ホームページには悪い評判がないので、忍者ホームページを選んだ。
2019年2月27日水曜日Yahoo!geocitiesから忍者ホーページhidesxima.ojaru.jpに引っ越し。
Yahoo!geocitiesから引っ越し。Yahoo!ジオシティーズから引っ越し。
2019年3月28日木曜日Yahoo!geocitiesから忍者ホーページhidesxima.ojaru.jpに転送設定。
2019年3月31日Yahoo!ジオシティーズのサービス終了